Boats and Streams problems are frequently asked problems in competitive exams.
Stream: Moving water of the river is called stream.
Still Water: If the water is not moving then it is called still water.
Upstream: If a boat or a swimmer moves in the opposite direction of the stream then it is called upstream.
Downstream: If a boat or a swimmer moves in the same direction of the stream then it is called downstream.
Points to remember
- When speed of boat or a swimmer is given then it normally means speed in still water.
Basic Formulas of Boats and Streams
Rule 1: If speed of boat or swimmer is x km/h and the speed of stream is y km/h then,
- Speed of boat or swimmer upstream = (x − y) km/h
- Speed of boat or swimmer downstream = (x + y) km/h
Rule 2:
- Speed of boat or swimmer in still water is given by
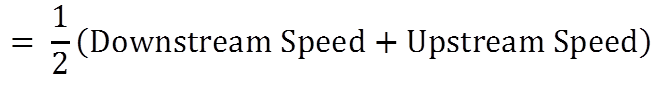
- Speed of stream is given by
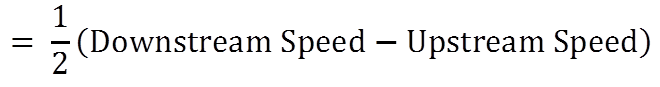
Shortcut methods for Boats and Streams
Rule 1: A man can row certain distance downstream in t1 hours and returns the same distance upstream in t2 hours. If the speed of stream is y km/h, then the speed of man in still water is given by
![]()
A man goes certain distance against the current of the stream in 2 hour and returns with the stream in 20 minutes. If the speed of stream is 4 km/h then how long will it take for the man to go 4 km in still water?
Sol:
Let’s say t1 = 20 minutes = 0.33 hours and t2 = 1 hours
Y = 4, then man’s speed in still water
![]()
So man’s speed is 7.94 km/h in still water.
Now, time taken by the man to row 4 km in still water
![]()
Rule 2: A man can row in still water at x km/h. In a stream flowing at y km/h, if it takes him t hours to row to a place and come back, then the distance between two places is given by
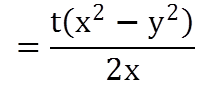
A man can row 4 km/h in still water. When the water is running at 2 km/h, it takes him 2 hours to go to a place and come back. What is the distance between that place and man’s initial position?
Sol:
Let’s say x = 4 km/h = man’s speed in still water.
y = 2 km/h = water’s speed.
t = 2, so
![]()
Rule 3: A man can row in still water at x km/h. In a stream flowing at y km/h, if it takes t hours more in upstream than to go downstream for the same distance, then the distance is given by
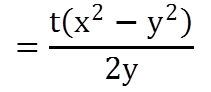
A man can row 4 km/h in still water. The water is running at 2 km/h. He travels to a certain distance and comes back. It takes him 2 hours more while travelling against the stream than travelling with the stream. What is the distance?
Sol:
Let’s say x = 4 km/h = man’s speed in still water.
y = 2 km/h = water’s speed.
t = 2, so
![]()
Rule 4: A man can row in still water at x km/h. In a stream flowing at y km/h, if he rows the same distance up and down the stream, then his average speed is given by
![]()
![]()
Speed of boat in still water is 9 km/h and speed of stream is 2 km/h. The boat rows to a place which is 47 km away and comes back in the same path. Find the average speed of boat during whole journey.
Sol:
Let’s say x = 9 km/h = speed in still water
Y = 2 km/h = speed of stream
![]()
