Problems on trains are most frequently asked questions in any competitive exam.
Problems on trains and ‘Time and Distance’ are almost same. The only difference is we have to consider the length of the train while solving problems on trains.
Points To Remember While Solving Problems On Trains
- Time taken by a train of length of L meters to pass a stationary pole is equal to the time taken by train to cover L meters.
- Time taken by a train of length of L meters to pass a stationary object of length P meters is equal to the time taken by train to cover (L + P) meters.
- If two trains are moving in same direction and their speeds are x km/h and y km/h (x > y) then their relative speed is (x – y) km/h.
- If two trains are moving in opposite direction and their speeds are x km/h and y km/h then their relative speed is (x + y) km/h.
Unit Conversion - kmph ⇔ mps
![]()
![]()
Shortcut Methods For Trains
Rule 1:
If two trains of p meters and q meters are moving in same direction at the speed of x m/s and y m/s (x > y) respectively then time taken by the faster train to overtake slower train is given by
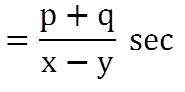
Two trains of length 130 meter and 70 meter are running in the same direction with the speed of 50 km/h and 70 km/h. How much time will faster train take to overtake the slower train from the moment they meet?
Sol:
Let’s say p = 130 meter = 0. 13 km
q = 70 meter = 0.07 km
x = 70 km/h and y = 50 km/h,
So from the equation given above,
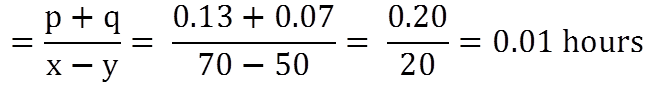
0.01 hours = 36 second
So it will take 36 seconds to overtake.
Rule 2:
If two trains of p meters and q meters are moving in opposite direction at the speed of x m/s and y m/s respectively then time taken by trains to cross each other is given by
![]()
Two trains of length 130 meter and 70 meter are running in the opposite direction with the speed of 50 km/h and 70 km/h. How much time will trains take to cross each other from the moment they meet?
Sol:
Let’s say p = 130 meter = 0. 13 km
q = 70 meter = 0.07 km
x = 70 km/h and y = 50 km/h,
So from the equation given above,
![]()
0.0017 hours = 6 seconds
So it will take 6 seconds to cross each other.
