Mixture: Mixing of two or more than two type of quantities gives us a mixure.
Quantities of these elements can be expressed as percentage or ratio.
i.e. Percentage (20% of sugar in water)
Fraction ( A solution of sugar and water such that sugar : water = 1:4)
Alligation: Alligation is a rule which is used to solve the problems related to mixture and its ingredient.
It is the rule that enables us to find the ratio in which two or more ingredients at the given price must be mixed to produce a mixture of desired price.
Alligation Rule
When two elements are mixed to make a mixture and one of the elements is cheaper and other one is costlier then,
![]()
Here Mean Price is CP of mixture per unit quantity.
Above rule can be written as,
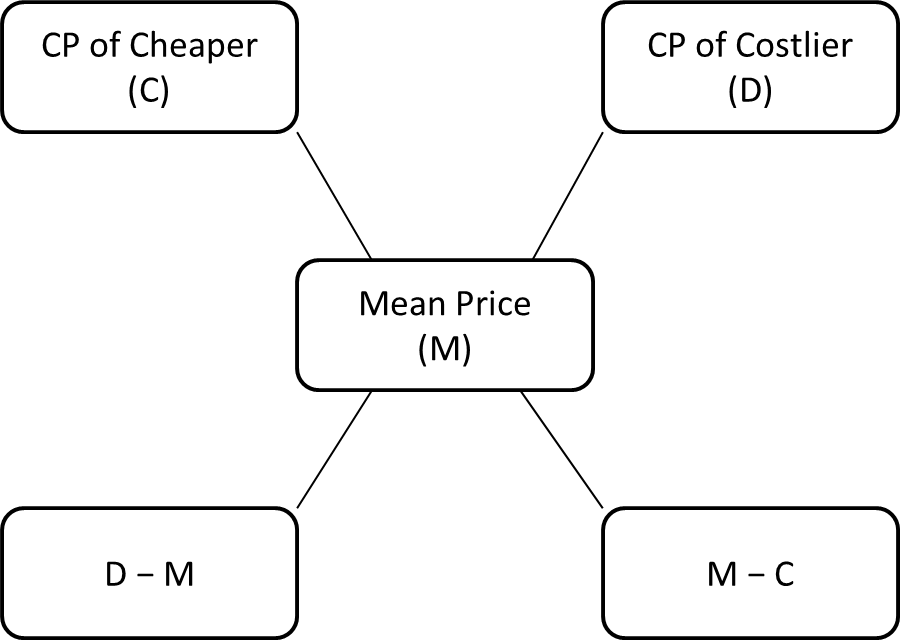
Then,
Cheaper Quantity : Costlier Quantity = (D – M) : (M – C)
In what proportion must sugar at Rs 40 per kg be mixed with sugar at Rs 60 per kg so that the mixture be Rs 55 per kg?
Sol:
Here, CP of Cheaper(C) = 40,
CP of Costlier(D) = 60 and
Mean Price(M) = 55
So from the rule of alligation we can say that
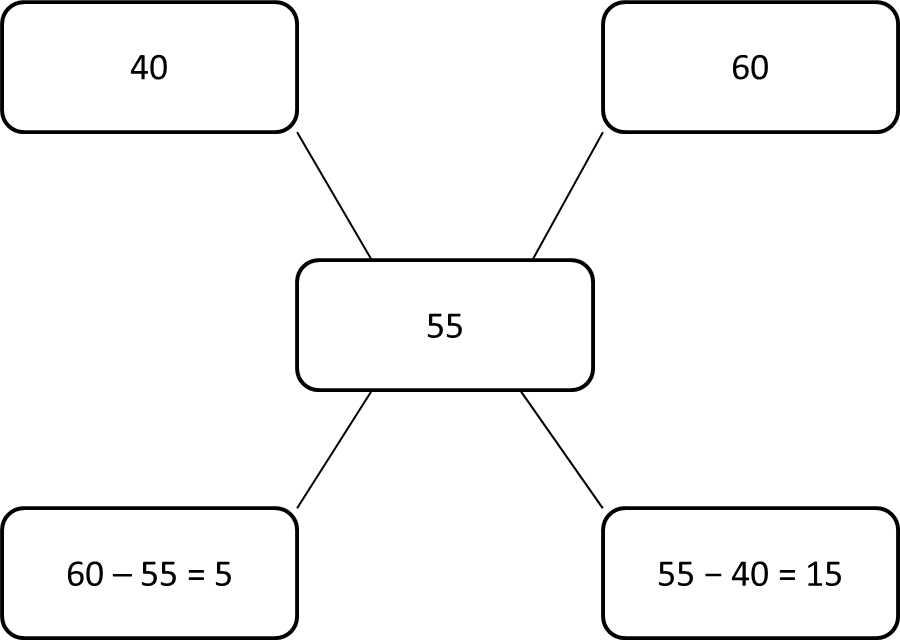
![]()
Proportion of Cheaper Sugar and Costlier Sugar is 1 : 3
Mixture of more than two elements.
This method is a bit tricky initially but if you practice it then it becomes quite easy.
If the mixture is of more than two ingredients, then write the prices of each ingredient below one another in ascending order. Write the mean price to the left of the list. Now make couples of prices in such a way that one price of the couple is below mean price and another price of the couple is above mean price. Now find the difference between each price and mean price and write it opposite to the price linked to it. This difference is required answer.
Don’t worry if you don’t understand above paragraph. Try to understand above paragraph with the examples given below.
How must a shop owner mix 4 types of rice worth Rs 95, Rs 60, Rs 90 and Rs 50 per kg so that he can make the mixture of these sugars worth Rs 80 per kg?
Sol:
Here the prices of sugars are 95, 60, 90 and 50.
And the mean price is 80.
Now read the above paragraph and the image given below to understand this method.
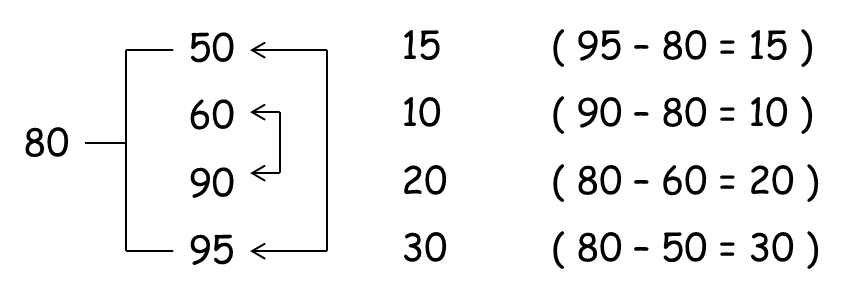
So the proportion of sugar is
50 : 60 : 90 : 95 = 15 : 10 : 20 : 30 or
50 : 60 : 90 : 95 = 3 : 2 : 4 : 6
In what ratio must a person mix three kind of tea each of which has a price of 70, 80 and 120 rupees per kg, in such a way that the mixture costs him 100 rupees per kg?
Sol:
Here the prices of tea are 70, 80 and 120
And mean price is 100, so
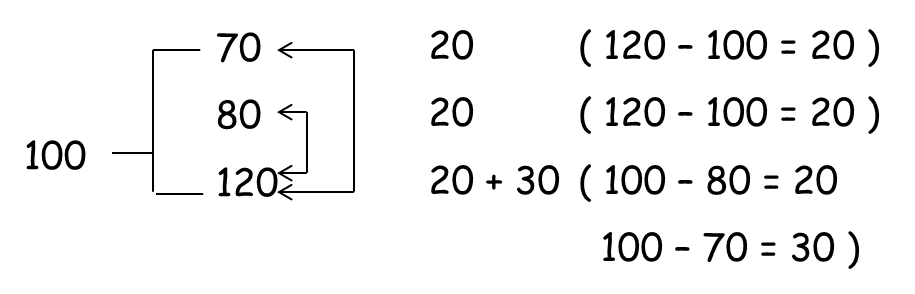
So the proportion of tea is
70 : 80 : 120 = 20 : 20 : 50 or
70 : 80 : 120 = 2 : 2 : 5
Shortcut Formulas for Mixture and Alligation
Rule 1
If n different vessels of equal size are filled with the mixture of P and Q in the ratio p1 : q1, p2 : q2, ……, pn : qn and content of all these vessels are mixed in one large vessel, then
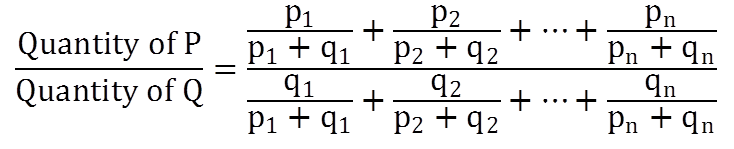
Three equal buckets containing the mixture of milk and water are mixed into a bigger bucket. If the proportion of milk and water in the glasses are 3:1, 2:3 and 4:2 then find the proportion of milk and water in the bigger bucket.
Sol:
Let’s say P stands for milk and Q stands for water,
So, p1:q1 = 3:1
p2:q2=2:3
p3 : q3=4:2
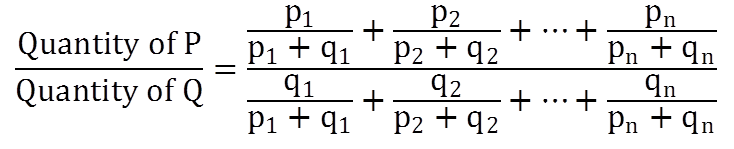
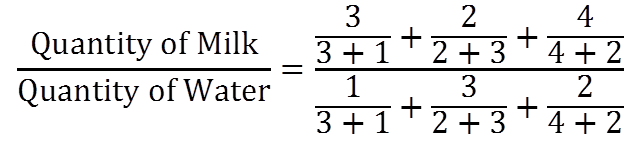
![]()
So in bigger bucket,
Milk : Water = 109 : 71
Rule 2
If n different vessels of sizes x1, x2, …, xn are filled with the mixture of P and Q in the ratio p1 : q1, p2 : q2, ……, pn : qn and content of all these vessels are mixed in one large vessel, then
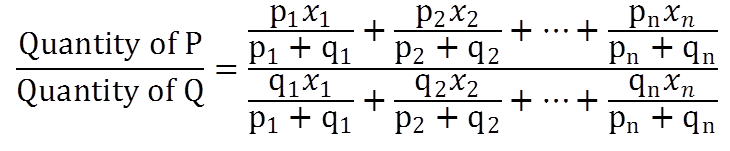
Three buckets of size 2 liter, 4 liter and 5 liter containing the mixture of milk and water are mixed into a bigger bucket. If the proportion of milk and water in the glasses are 3:1, 2:3 and 4:2 then find the proportion of milk and water in the bigger bucket.
Sol:
Let’s say P stands for milk and Q stands for water,
So, p1:q1 = 3:1 , x1 = 2
p2:q2=2:3 , x2 = 4
p3 : q3=4:2 x3 = 5, so
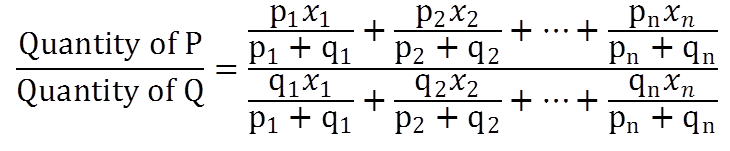
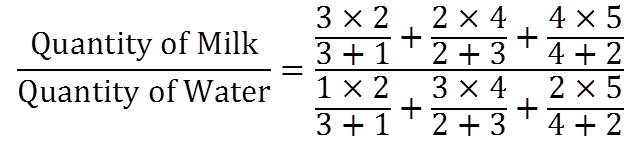
![]()
So in bigger bucket,
Milk : Water = 193 : 137
Rule 3: Removal and Replacement
If a vessel contains “x” litres of liquid A and if “y” litres be withdrawn and replaced by liquid B, then if “y” litres of the mixture be withdrawn and replaced by liquid B, and the operation is repeated ‘n’ times in all, then :
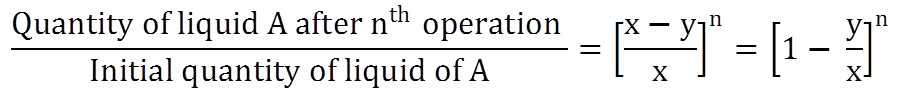
A container is containing 80 liter of wine. 8 liter of wine was taken out from this container and replaced by water. This process was further repeated two times. How much wine is there in the container now?
Sol:
Here x = 80, y = 8 and n = 3, so
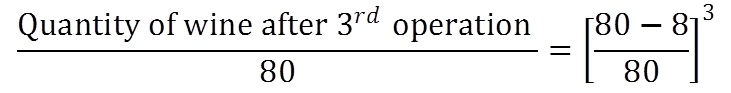
Quantity of wine after 3rd operation = 58.32 liters.
Rule 4:
p gram of ingredient solution has a% ingredient in it. To increase the ingredient content to b% in the solution
![]()
125 liter of mixture of milk and water contains 25% of water. How much water must be added to it to make water 30% in the new mixture?
Sol:
Let’s say p = 125, b = 30, a = 25
So from the equation
![]()
Quantity of water need to be added = 8.92 liter.
