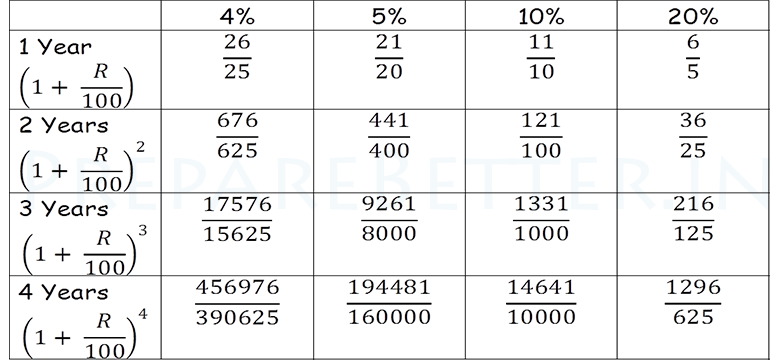In compound interest, the interest for each period is added to the principle before interest is calculated for the next period. With this method the principle grows as the interest is added to it. This method is mostly used in investments such as savings account and bonds.
To understand compound interest clearly, let’s take an example.
1000 is borrowed for three years at 10% compound interest. What is the total amount after three years?
You can understand the process of compound interest by image shown below.
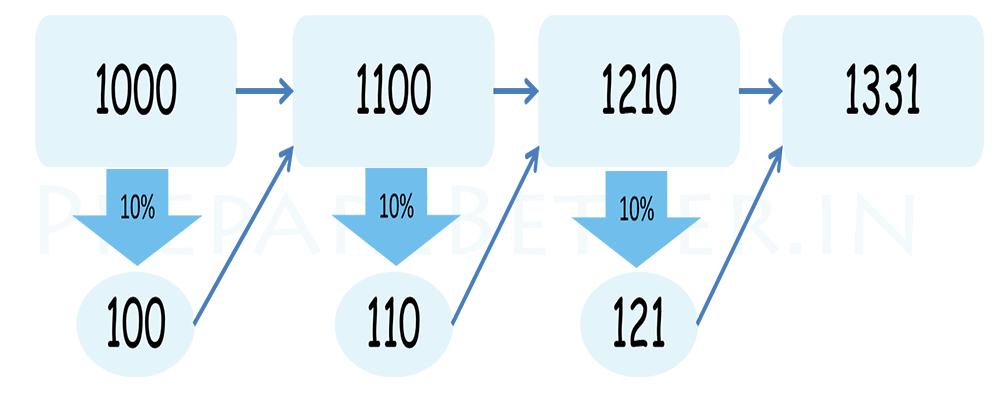
|
Year |
Principle |
Interest (10%) |
Amount |
|
1st |
1000 |
100 |
1100 |
|
2nd |
1100 |
110 |
1210 |
|
3rd |
1210 |
121 |
1331 |
Difference between Simple Interest and compound interest
After three years,
In simple interest, the total amount would be 1300
And in compound interest, the total amount would be 1331.
Basic Formulas of Compound Interest
If A = Amount
P = Principle
C.I. = Compound Interest
T = Time in years
R = Interest Rate Per Year
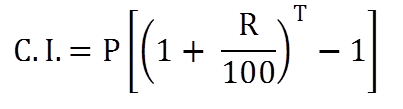
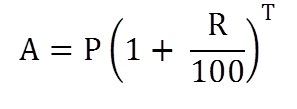
Shortcut Formulas for Compound Interest
Rule 1: If rate of interest is R1% for first year, R2% for second year and R3% for third year, then
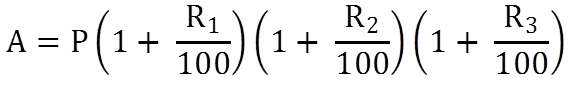
Find the total amount after three years on Rs 1000 if the compound interest rate for first year is 4%, for second year is 5% and for third year is 10%
Sol:
P = 1000
R1 = 4%, R2 = 5% and R3 = 10%
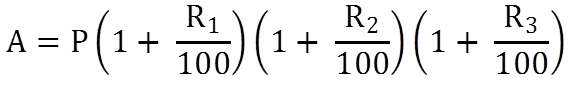
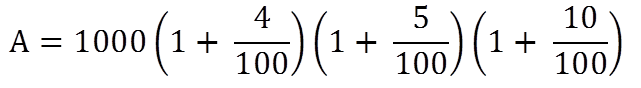
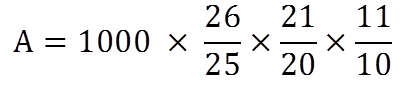
(From the table given at the bottom of the page)
A = 1201.2
Rule 2:
If principle = P, Rate = R% and Time = T years then
- If the interest is compounded annually:
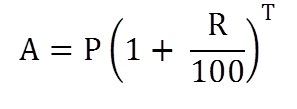
- If the interest is compounded half yearly (two times in year):
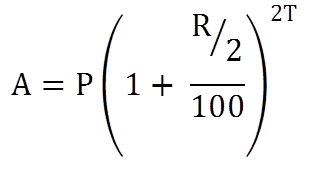
- If the interest is compounded quarterly (four times in year):
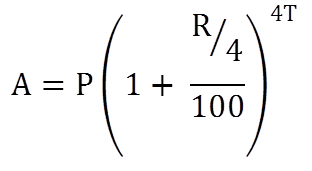
Find the total amount on 1000 after 2 years at the rate of 4% if
- The interest is compounded annually
- The interest is compounded half yearly
- The interest is compounded quarterly.
Sol:
Here P = 1000
R = 4%
T = 2 years
If the interest is compounded annually
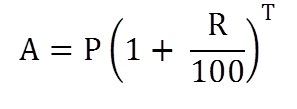
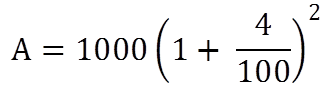
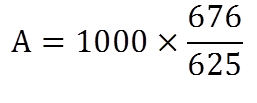
(From the table given at the bottom of the page)
A = 1081.6
If the interest is compounded half yearly
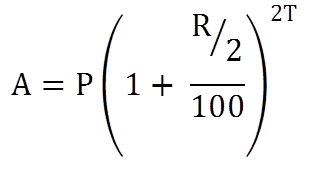
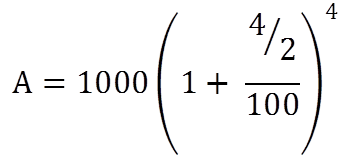
A = 1082.4
If the interest is compounded quarterly
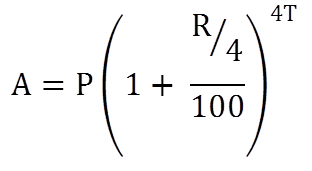
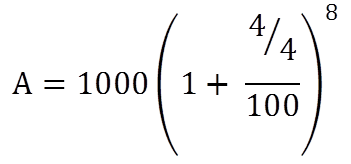
A = 1082.9
Rule 3: If difference between Simple Interest and Compound Interest is given.
- If the difference between Simple Interest and Compound Interest on a certain sum of money for 2 years at R% rate is given then

If the difference between simple interest and compound interest on a certain sum of money at 10% per annum for 2 years is Rs 2 then find the sum.
Sum:

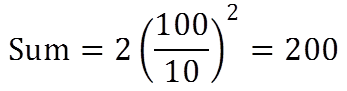
- If the difference between Simple Interest and Compound Interest on a certain sum of money for 3 years at R% is given then
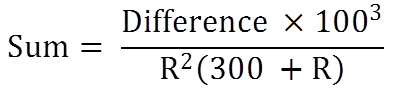
If the difference between simple interest and compound interest on a certain sum of money at 10% per annum for 3 years is Rs 2 then find the sum.
Sol:
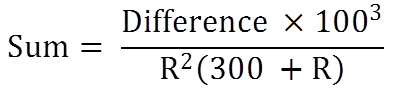
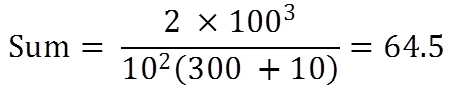
Rule 4: If sum A becomes B in T1 years at compound interest, then after T2 years
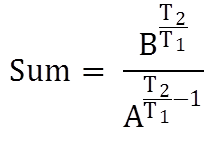
Rs 1000 becomes 1100 after 4 years at certain compound interest rate. What will be the sum after 8 years?
Sum:
Here A = 1000, B = 1100
T1 = 4, T2 = 8
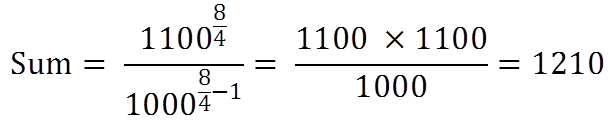
Look up Table