You can find square of any number in the world with this method.
Let’s say the number is two digit number. i.e. AB.
So B is units digit and A is tens digit.
Step 1: Find Square of B
Step 2: Find 2×A×B
Step 3: Find Square of A
Let’s take an example.
We want to find square of 37.
Step 1: Find square of 7.
Square of 7 = 49.
So write 9 in the answer and 4 as carry to the second step.
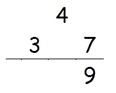
Step 2: Find 2×(3×7)
2 × (3 × 7) = 42.
42 + 4(Carry) = 46.
Write 6 in the answer and 4 as a carry to the third step.
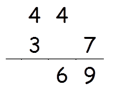
Step 3: Find square of 3
Square of 3 = 9
9 + 4(Carry) = 13.
Write 13 in the answer.
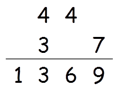
So the answer is 1369.
Now, If the number is of three digit i.e. ABC
Here C is unit’s digit, B is ten’s digit and A is hundredth digit.
Step 1: Find Square of C
Step 2: Find 2 × (B × C)
Step 3: Find 2 × (A × C) + B2
(NOTE: You may observe that in odd number of digit case, we are multiplying end two digits with 2 (here: A and C) and squaring single digit (here B).
Step 4: Find 2 × (A × B)
(NOTE: You may observe that whenever there are double digits, we are multiplying it with 2. And whenever there is single digit, we are squaring it.)
Step 5: Find square of A
(NOTE: Here is single digit, so we are squaring it.)
Let’s take an example.
Find square of 456.
Step 1: Find square of 6.
Square of 6 = 36.
So write 6 in the answer and 3 as a carry to the second step.
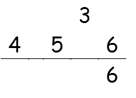
Step 2: Find 2 × (5 × 6)
2 × (5 × 6) = 60
60 + 3(Carry) = 63
Write 3 in the answer and 6 as a carry to the third step.
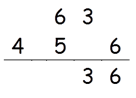
Step 3: Find 2 × (4 × 6) + 52
2 × (4 × 6) + 52 = 73
73 + 6(Carry) = 79
Write 9 in the answer and 7 as a carry to the fourth step.
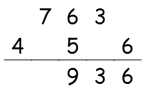
Step 4: Find 2 × (4 × 5)
2 × (4 × 5) = 40
40 + 7 = 47
Write 7 in the answer and 4 as a carry to the fifth step.
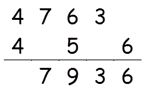
Step 5: Find square of 4
Square of 4 = 16
16 + 4(Carry) = 20
Write 20 in the answer.
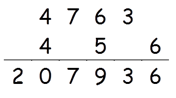
So 4562 = 207936.
Now, If the number is of four digit i.e. ABCD
Here D is unit’s digit, C is ten’s digit, B is hundredth digit and A is thousands digit.
Step 1: Find Square of D
Step 2: Find 2 × (C × D)
Step 3: Find 2 × (B × D) + C2
(NOTE: You may observe that in odd number of digit case, we are multiplying end two digits with 2 (here: B and D) and squaring single remaining digit (here C).
Step 4: Find 2 × (A × D) + 2 × (B × C)
(NOTE: You may observe that where ever there is even digits, we are multiplying end two digits with 2 + remaining two digits with 2.)
Step 5: Find 2 × (A × C) + B2
(NOTE: You may observe that in odd number of digit case, we are multiplying end two digits with 2 (here: A and C) and squaring single remaining digit (here B).
Step 6: Find 2 × (A × B)
(NOTE: You may observe that here even digits so we are multiplying them with 2, and no remaining digits so we are not adding anything.)
Step 7: Find square of A
Let’s take an example.
Find square of 1234
Step 1: Find Square of 4
Square of 4 = 16
So write 6 in the answer and 1 as a carry to the second step.
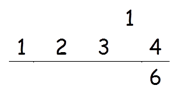
Step 2: Find 2 × (3 × 4)
2 × (3 × 4) = 24
24 + 1(Carry) = 25
Write 5 in the answer and 2 as a carry to the third step
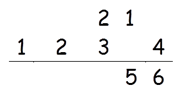
Step 3: Find 2 × (2 × 4) + 32
2 × (2 × 4) + 32 = 25
25 + 2(Carry) = 27
Write 7 in the answer and 2 as a carry to the fourth step.
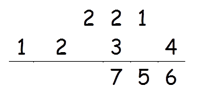
Step 4: Find 2 × (1 × 4) + 2 × (2 × 3)
2 × (1 × 4) + 2 × (2 × 3) = 20
20 + 2(Carry) = 22
Write 2 in the answer and 2 as a carry to the fifth step.
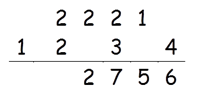
Step 5: Find 2 × (1 × 3) + 22
2 × (1 × 3) + 22 = 10
10 + 2(Carry) = 12
Write 2 in the answer and 1 as carry to the sixth step.
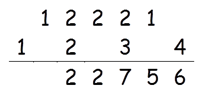
Step 6: Find 2 × (1 × 2)
2 × (1 × 2) = 4
4 + 1(Carry) = 5
Write 5 in the answer
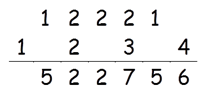
Step 7: Find square of 1
Square of 1 = 1
There is no carry so write 1 in the answer.
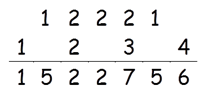
So, 12342 = 1522756
